Hex Password Generator
Introduction:
The Hex Password Generator is a small program used to create Random Passwords. In the Standard mode
it uses Characters from A to Z, and lower case a to z, and numbers from 0 to 9. In Enhanced mode it
adds 10 Special Characters, ! @ # $ % ( ) <> ? for sites that allow, or require them. From what I
have read, it’s good to have Passwords based on Entropy. The Hex Password Generator is a small
program used to create Random Passwords. In the Standard mode it uses Characters from A to Z,
and
lower case a to z, and numbers from 0 to 9. In Enhanced mode it adds 10 Special Characters,
! @ # $ % ( ) <> ? for sites that allow, or require them. From what I have read, it’s good to
have
Passwords based on Entropy. Entropy is, Length and Probability, that is the number of
characters
and how many different characters are involved.
The formula for Entropy is: H = L * log(N) / log(2) Where H is Entropy, L is Length and N is
the number of characters. The higher the Entropy, the safer your password. Let’s say you
have a
pool of 62 different characters, the same as the standard mode of this program,
(26*2+10=62).
For each characters you have an Entropy of 6 bits, (log(62) / log(2) = 5.95). You might ask
if this is always true, and it is not. If you use a password of “Password” it would give you
Entropy of 46 bits, but that password is still very easy to crack because of the way
password
crackers are deployed. Entropy is, Length and Probability, that is the number of characters
and
how many different characters are involved.
The formula for Entropy is: H = L * log(N) / log(2) Where H is Entropy, L is Length and N is
the
number of characters. The higher the Entropy, the safer your password. Let’s say you have a
pool
of 62 different characters, the same as the standard mode of this program, (26*2+10=62). For
each
characters you have an Entropy of 6 bits, (log(62) / log(2) = 5.95). You might ask if this
is always
true, and it is not. If you use a password of “Password” it would give you Entropy of 46
bits,
but that password is still very easy to crack because of the way password crackers are
deployed.
| Type | Pool of Characters Possible |
|---|---|
| Lowercase | 26 |
| Lower & Upper Case | 52 |
| Alphanumeric | 36 |
| Alphanumeric & Upper Case | 62 |
| Common ASCII Characters | 30 |
| Diceware Words List | 7,776 |
| English Dictionary Words | 1,022,000 and counting |
That is the reason I wrote this program.
While there are other ways to come up with a Random Passwords, such as a Password Card found at: PasswordCard.org, I just found this a better way for me. Since I didn’t encrypt the passwords generated, it’s best to store the passwords you generate on an external drive, such as a thumb drive or external hard drive that can be disconnected from your computer, and stored in a safe or another safe place.
The Program:
| # of Characters | Entropy Standard | Entropy Enhanced |
|---|---|---|
| 8 | 48 | 49 |
| 9 | 54 | 55 |
| 10 | 60 | 62 |
| 11 | 65 | 68 |
| 12 | 71 | 74 |
| 13 | 77 | 80 |
| 14 | 83 | 86 |
| 15 | 89 | 93 |
| 16 | 95 | 99 |
| 17 | 101 | 105 |
| 18 | 107 | 111 |
| 19 | 113 | 117 |
| 20 | 119 | 123 |
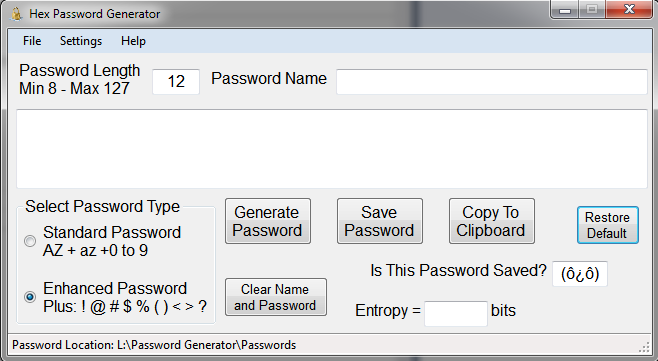 This is the Hex Password Generator.
When you are ready to use the program, you start by giving the password a Name, as this is so
you know what the password belongs too.
Password Length can be changed manually, or set in the Settings Menu, (to be covered later in
this document). You can select the Password Type either Standard or Enhanced,
and then you can Generate your Password. You can Save your Password to the file, and also copy
to your clipboard to paste it into the site you’re generating the password for.
This will also tell you if the password has been saved or not, so that you know at a glance if
you saved it.
This is the Hex Password Generator.
When you are ready to use the program, you start by giving the password a Name, as this is so
you know what the password belongs too.
Password Length can be changed manually, or set in the Settings Menu, (to be covered later in
this document). You can select the Password Type either Standard or Enhanced,
and then you can Generate your Password. You can Save your Password to the file, and also copy
to your clipboard to paste it into the site you’re generating the password for.
This will also tell you if the password has been saved or not, so that you know at a glance if
you saved it.
If by chance you have changed the password location to an external
drive, and you do not connect the drive before you start the program, you will first get this
informational popup.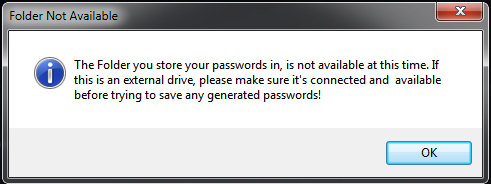 When you hit OK, the program will start up as normal. You will still be able to generate
passwords, but you can’t save them until the external drive is connected and ready for use.
The Password Location is listed at the bottom of the program in the Status Bar. (See Program
picture above)
When you hit OK, the program will start up as normal. You will still be able to generate
passwords, but you can’t save them until the external drive is connected and ready for use.
The Password Location is listed at the bottom of the program in the Status Bar. (See Program
picture above)
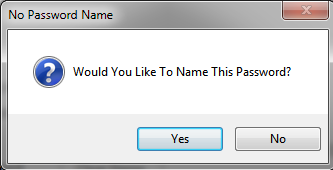
Because Passwords are of such importance, if you didn’t name your
password, the program will remind you, but you can still save the password without a name. If
you hit “Yes”, you will be taken back to the program without saving the password,
and you can enter a name for the password, and if you hit “No” the password will be saved
without a Name.
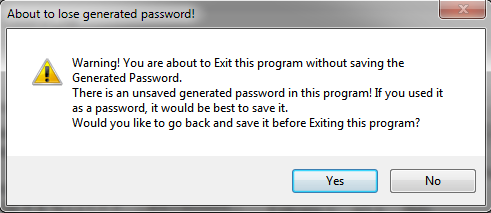
Likewise, if you generated a password, and didn’t save it and try to Exit the program, you will
get a warning letting you know you are about to lose your password. Hitting
“Yes will take you back to the program and cancel the closing so you can save
your password, and hitting “No” will Exit the program without saving your password.
It may seem that there are a lot of Question and Warnings popup windows in this program, but
they are there only for the protection of the generated passwords, and so you don’t
lose a password you created and used with this program.
Configure:
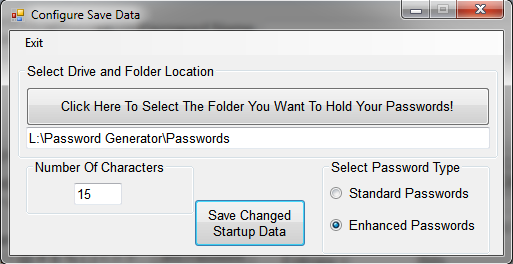 Under the “Settings” on the menu bar, you will
find “Configure”. Clicking on Configure will bring up this Window.
Here you can set your Password Folder location, and the number of characters, and what password type you
want to start the program with. Each time you start up the program,
it will use these settings. In the program itself, you can always change the password type and number of
characters, but not the location of where you store the saved passwords.
You don’t have to worry about your password file when you change the location as your password file is
moved to the new location when you hit the Save Changed Startup Data. If the
current folder is on an external drive, and you try to change the location without having the drive
connected and ready for use, you will get a warning letting you know about it.
It will give you the option of changing the location without moving your old password file. That is not
a good idea, and if you chose to change the location without moving the old
password file, then you start a new password file with your next saved password.
The main thing to remember is that if you use an external drive, you always want your password drive
connected and ready to use when starting up this program. Things go much smoother when everything is in
place and ready for new passwords.
Under the “Settings” on the menu bar, you will
find “Configure”. Clicking on Configure will bring up this Window.
Here you can set your Password Folder location, and the number of characters, and what password type you
want to start the program with. Each time you start up the program,
it will use these settings. In the program itself, you can always change the password type and number of
characters, but not the location of where you store the saved passwords.
You don’t have to worry about your password file when you change the location as your password file is
moved to the new location when you hit the Save Changed Startup Data. If the
current folder is on an external drive, and you try to change the location without having the drive
connected and ready for use, you will get a warning letting you know about it.
It will give you the option of changing the location without moving your old password file. That is not
a good idea, and if you chose to change the location without moving the old
password file, then you start a new password file with your next saved password.
The main thing to remember is that if you use an external drive, you always want your password drive
connected and ready to use when starting up this program. Things go much smoother when everything is in
place and ready for new passwords.
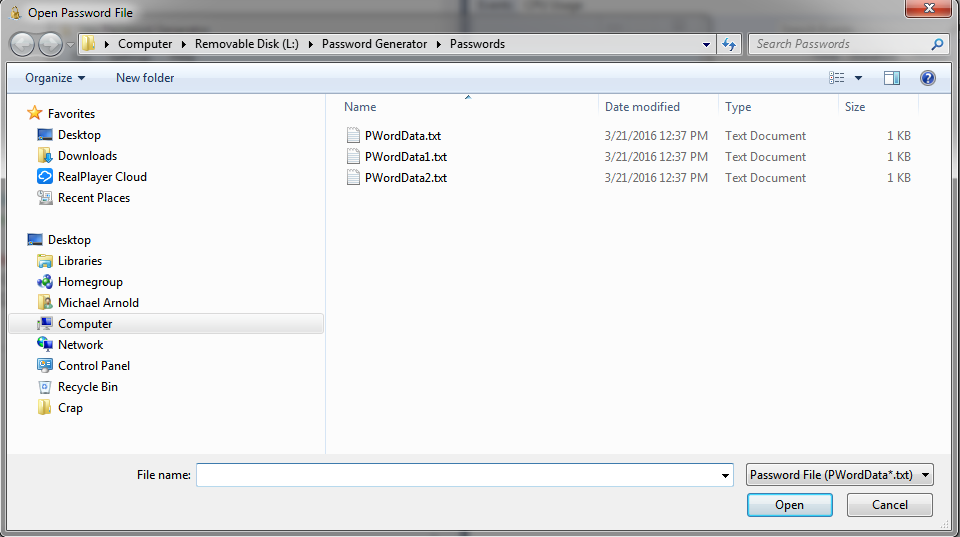
Open File: